RLT Package: Regression With Reinforcement Learning and Linear Combination Splits
Ruoqing Zhu
Last Updated: July 17, 2025
Test-RLT-Reg.RmdInstall and Load Package
Install and load the GitHub version of the RLT package. Do not use the CRAN version.
Single Variable Embedded Splitting
When reinforcement is enabled, an embedded random forest
model and the corresponding variable importance measure will be used to
search for the best splitting rule. There will be a default setting of
parameters for the embedded model, however you can still tune them
individually.
set.seed(2)
n = 1000
p = 10
X = matrix(rnorm(n*p), n, p)
y = 1 + X[, 1] + X[, 3] + X[, 9] + rnorm(n)
testX = matrix(rnorm(n*p), n, p)
testy = 1 + testX[, 1] + testX[, 3] + testX[, 9] + rnorm(n)
start_time <- Sys.time()
RLTfit <- RLT(X, y, model = "regression",
ntrees = 100, ncores = 1, nmin = 10,
split.gen = "random", nsplit = 1,
resample.prob = 0.85, resample.replace = FALSE,
reinforcement = TRUE, importance = "distribute",
param.control = list("embed.ntrees" = 50,
"embed.mtry" = 1/2,
"embed.nmin" = 5),
verbose = TRUE)
## Regression Random Forest ...
## ---------- Parameters Summary ----------
## (N, P) = (1000, 10)
## # of trees = 100
## (mtry, nmin) = (3, 10)
## split generate = Random, 1
## sampling = 0.85 w/o replace
## (Obs, Var) weights = (No, No)
## importance = distribute
## reinforcement = Yes
## ----------------------------------------
## embed.ntrees = 50
## embed.mtry = 50%
## embed.nmin = 5
## embed.split.gen = Random, 1
## embed.resample.replace = TRUE
## embed.resample.prob = 0.9
## embed.mute = 0
## embed.protect = 14
## embed.threshold = 0.25
## ----------------------------------------
difftime(Sys.time(), start_time, units = "secs")
## Time difference of 56.29952 secs
# oob error
mean((RLTfit$Prediction - y)^2, na.rm = TRUE)
## [1] 1.332247
# prediction error
pred = predict(RLTfit, testX)
mean((pred$Prediction - testy)^2)
## [1] 1.279387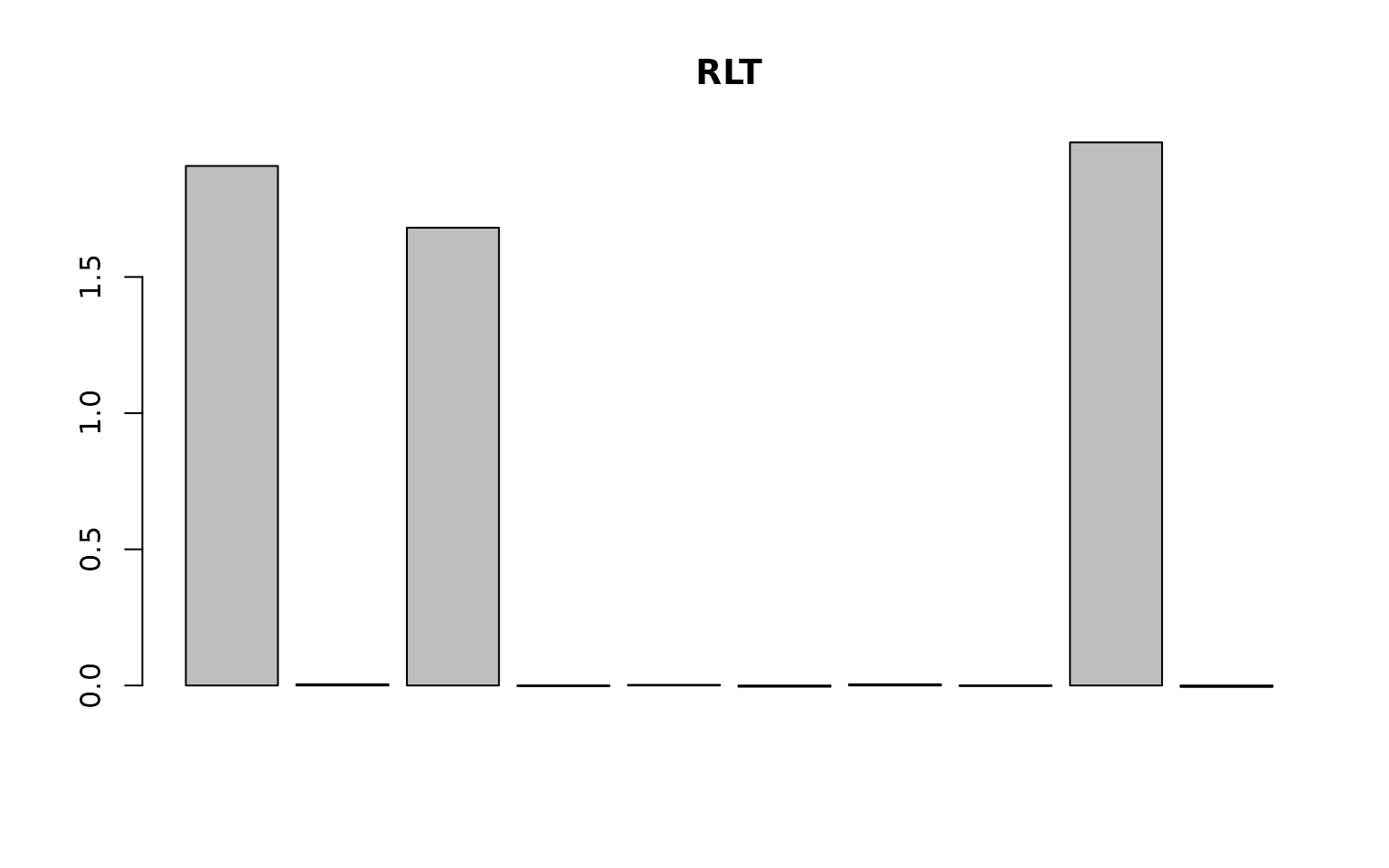
# check one tree
get.one.tree(RLTfit, 1)
## Tree #1 in the fitted regression forest:
## SplitVar SplitValue LeftNode RightNode NodeWeight NodeAve
## 1 V 1 -0.980294208 2 3 850 0.000000000
## 2 V 3 1.081845086 4 5 128 0.000000000
## 3 V 9 -1.975008396 42 43 722 0.000000000
## 4 V 9 -0.567707078 6 7 109 0.000000000
## 5 V 9 -3.314706284 38 39 19 0.000000000
## 6 V 3 -0.166537182 8 9 40 0.000000000
## 7 V 3 -0.227713509 20 21 69 0.000000000
## 8 V 9 -1.057140123 10 11 21 0.000000000
## 9 V 4 0.129346882 14 15 19 0.000000000
## 10 <NA> NA NA NA 9 -2.946581367
## 11 V 10 -0.965233503 12 13 12 0.000000000
## 12 <NA> NA NA NA 3 -2.357358172
## 13 <NA> NA NA NA 9 -1.413073684
## 14 V 4 -1.475830364 16 17 13 0.000000000
## 15 <NA> NA NA NA 6 -2.569854211
## 16 <NA> NA NA NA 1 -0.404507502
## 17 V 4 -1.041379040 18 19 12 0.000000000
## 18 <NA> NA NA NA 4 -0.795853226
## 19 <NA> NA NA NA 8 -1.597350858
## 20 V 3 -1.068702106 22 23 33 0.000000000
## 21 V 9 -0.432333301 26 27 36 0.000000000
## 22 V 1 -2.099225632 24 25 11 0.000000000
## 23 <NA> NA NA NA 22 -0.307904267
## 24 <NA> NA NA NA 2 -2.892655219
## 25 <NA> NA NA NA 9 -2.312824540
## 26 <NA> NA NA NA 2 0.347616707
## 27 V 9 0.063996427 28 29 34 0.000000000
## 28 <NA> NA NA NA 10 -0.311221632
## 29 V 5 0.888988473 30 31 24 0.000000000
## 30 V 5 -1.209662195 32 33 21 0.000000000
## 31 <NA> NA NA NA 3 1.352770278
## 32 <NA> NA NA NA 2 -0.989977059
## 33 V 3 -0.059455969 34 35 19 0.000000000
## 34 <NA> NA NA NA 5 -0.128353622
## 35 V 5 -0.229565449 36 37 14 0.000000000
## 36 <NA> NA NA NA 8 1.171801487
## 37 <NA> NA NA NA 6 0.667392199
## 38 <NA> NA NA NA 1 -3.210977199
## 39 V 5 -0.747214107 40 41 18 0.000000000
## 40 <NA> NA NA NA 9 1.278504984
## 41 <NA> NA NA NA 9 0.790146990
## 42 V 1 -0.012259387 44 45 22 0.000000000
## 43 V 9 -0.342721271 48 49 700 0.000000000
## 44 <NA> NA NA NA 10 -2.144898360
## 45 V 1 0.372123840 46 47 12 0.000000000
## 46 <NA> NA NA NA 3 -1.609794044
## 47 <NA> NA NA NA 9 -0.491322769
## 48 V 3 0.943714876 50 51 249 0.000000000
## 49 V 3 -0.390820753 130 131 451 0.000000000
## 50 V 1 -0.948187756 52 53 209 0.000000000
## 51 V 1 0.364553558 124 125 40 0.000000000
## 52 <NA> NA NA NA 2 -2.086041019
## 53 V 1 -0.381395987 54 55 207 0.000000000
## 54 V 3 0.840826107 56 57 48 0.000000000
## 55 V 1 0.069347145 72 73 159 0.000000000
## 56 V 3 0.494422039 58 59 47 0.000000000
## 57 <NA> NA NA NA 1 -0.045884843
## 58 V 3 -0.592980770 60 61 39 0.000000000
## 59 <NA> NA NA NA 8 -0.131433235
## 60 V 3 -0.693980785 62 63 16 0.000000000
## 61 V 8 0.366139663 66 67 23 0.000000000
## 62 V 3 -1.249552132 64 65 15 0.000000000
## 63 <NA> NA NA NA 1 -0.379246393
## 64 <NA> NA NA NA 9 -1.656711905
## 65 <NA> NA NA NA 6 -0.418339252
## 66 V 7 0.844452684 68 69 11 0.000000000
## 67 V 5 -0.038589072 70 71 12 0.000000000
## 68 <NA> NA NA NA 10 -0.722036381
## 69 <NA> NA NA NA 1 -0.433014076
## 70 <NA> NA NA NA 7 -0.631405423
## 71 <NA> NA NA NA 5 -1.106582171
## 72 V 3 0.253750270 74 75 46 0.000000000
## 73 V 1 1.176608935 88 89 113 0.000000000
## 74 V 3 -1.402474593 76 77 30 0.000000000
## 75 V 9 -0.870533884 86 87 16 0.000000000
## 76 <NA> NA NA NA 5 -2.292160534
## 77 V 9 -1.248944399 78 79 25 0.000000000
## 78 <NA> NA NA NA 9 -0.821608795
## 79 V 4 -0.707155481 80 81 16 0.000000000
## 80 <NA> NA NA NA 2 -1.410490863
## 81 V 4 0.541512747 82 83 14 0.000000000
## 82 V 4 -0.360714757 84 85 11 0.000000000
## 83 <NA> NA NA NA 3 -1.016217441
## 84 <NA> NA NA NA 3 0.956852740
## 85 <NA> NA NA NA 8 -0.177579922
## 86 <NA> NA NA NA 10 -0.445508047
## 87 <NA> NA NA NA 6 1.362056300
## 88 V 9 -0.414155432 90 91 77 0.000000000
## 89 V 7 -1.310902523 112 113 36 0.000000000
## 90 V 9 -0.704789443 92 93 74 0.000000000
## 91 <NA> NA NA NA 3 0.822624630
## 92 V 9 -1.334623845 94 95 49 0.000000000
## 93 V 3 0.502624752 106 107 25 0.000000000
## 94 V 3 -0.587525038 96 97 20 0.000000000
## 95 V 5 -0.588941176 100 101 29 0.000000000
## 96 <NA> NA NA NA 3 -2.101852726
## 97 V 9 -1.546749861 98 99 17 0.000000000
## 98 <NA> NA NA NA 9 -0.377257958
## 99 <NA> NA NA NA 8 0.502438622
## 100 <NA> NA NA NA 12 -0.152758117
## 101 V 6 0.188828891 102 103 17 0.000000000
## 102 V 3 0.371449427 104 105 11 0.000000000
## 103 <NA> NA NA NA 6 1.351209989
## 104 <NA> NA NA NA 7 0.124928479
## 105 <NA> NA NA NA 4 1.406889173
## 106 V 3 -0.254496482 108 109 22 0.000000000
## 107 <NA> NA NA NA 3 1.600456857
## 108 V 8 -0.608467484 110 111 14 0.000000000
## 109 <NA> NA NA NA 8 1.240444565
## 110 <NA> NA NA NA 6 0.830417982
## 111 <NA> NA NA NA 8 -0.208581743
## 112 <NA> NA NA NA 4 1.602902041
## 113 V 3 0.740537784 114 115 32 0.000000000
## 114 V 9 -0.432452981 116 117 28 0.000000000
## 115 <NA> NA NA NA 4 3.109474634
## 116 V 9 -1.529638071 118 119 27 0.000000000
## 117 <NA> NA NA NA 1 -0.588311255
## 118 <NA> NA NA NA 3 1.059922330
## 119 V 9 -0.758692636 120 121 24 0.000000000
## 120 V 3 -1.072888333 122 123 14 0.000000000
## 121 <NA> NA NA NA 10 2.265950232
## 122 <NA> NA NA NA 2 -0.159231460
## 123 <NA> NA NA NA 12 1.259372165
## 124 <NA> NA NA NA 25 1.274163571
## 125 V 7 -1.156705580 126 127 15 0.000000000
## 126 <NA> NA NA NA 1 5.203009807
## 127 V 6 0.448026134 128 129 14 0.000000000
## 128 <NA> NA NA NA 11 2.494537473
## 129 <NA> NA NA NA 3 2.466676960
## 130 V 9 -0.164446376 132 133 141 0.000000000
## 131 V 1 1.421779808 168 169 310 0.000000000
## 132 V 1 1.092478657 134 135 22 0.000000000
## 133 V 1 0.667522687 138 139 119 0.000000000
## 134 V 1 0.290622192 136 137 20 0.000000000
## 135 <NA> NA NA NA 2 0.748583516
## 136 <NA> NA NA NA 13 -1.068779685
## 137 <NA> NA NA NA 7 0.316972118
## 138 V 9 2.145745584 140 141 74 0.000000000
## 139 V 3 -0.968510334 162 163 45 0.000000000
## 140 V 9 0.378459341 142 143 72 0.000000000
## 141 <NA> NA NA NA 2 2.861149330
## 142 V 3 -1.026005198 144 145 24 0.000000000
## 143 V 1 -0.601160105 148 149 48 0.000000000
## 144 V 3 -1.784254983 146 147 14 0.000000000
## 145 <NA> NA NA NA 10 0.352463908
## 146 <NA> NA NA NA 7 -1.342753577
## 147 <NA> NA NA NA 7 -0.478125604
## 148 <NA> NA NA NA 10 0.452243129
## 149 V 1 -0.269269376 150 151 38 0.000000000
## 150 V 3 -2.031660362 152 153 12 0.000000000
## 151 V 1 -0.249391973 156 157 26 0.000000000
## 152 <NA> NA NA NA 1 -0.161411369
## 153 V 3 -0.694417185 154 155 11 0.000000000
## 154 <NA> NA NA NA 10 0.918789555
## 155 <NA> NA NA NA 1 0.373254813
## 156 <NA> NA NA NA 1 0.304052770
## 157 V 1 0.302551135 158 159 25 0.000000000
## 158 V 4 -0.768414248 160 161 15 0.000000000
## 159 <NA> NA NA NA 10 2.090603844
## 160 <NA> NA NA NA 8 0.257445331
## 161 <NA> NA NA NA 7 1.727717773
## 162 V 5 0.950067905 164 165 28 0.000000000
## 163 V 3 -0.769979488 166 167 17 0.000000000
## 164 <NA> NA NA NA 21 1.560635190
## 165 <NA> NA NA NA 7 1.387853122
## 166 <NA> NA NA NA 7 1.241767160
## 167 <NA> NA NA NA 10 3.155629542
## 168 V 1 0.790544664 170 171 275 0.000000000
## 169 V 9 0.623554849 258 259 35 0.000000000
## 170 V 3 -0.084940836 172 173 223 0.000000000
## 171 V 3 0.763312927 244 245 52 0.000000000
## 172 V 9 1.081387426 174 175 36 0.000000000
## 173 V 3 2.051815273 186 187 187 0.000000000
## 174 V 9 0.270557457 176 177 28 0.000000000
## 175 <NA> NA NA NA 8 2.646220066
## 176 V 8 -0.750501199 178 179 15 0.000000000
## 177 V 1 -0.471508188 184 185 13 0.000000000
## 178 <NA> NA NA NA 1 -1.433253766
## 179 V 7 -2.138510389 180 181 14 0.000000000
## 180 <NA> NA NA NA 1 -0.079023630
## 181 V 8 0.943044327 182 183 13 0.000000000
## 182 <NA> NA NA NA 10 0.272021119
## 183 <NA> NA NA NA 3 2.611826807
## 184 <NA> NA NA NA 3 -0.052476521
## 185 <NA> NA NA NA 10 2.277160016
## 186 V 9 1.343866134 188 189 178 0.000000000
## 187 <NA> NA NA NA 9 4.222427173
## 188 V 3 1.332984816 190 191 167 0.000000000
## 189 V 10 -1.350376528 242 243 11 0.000000000
## 190 V 3 1.136046868 192 193 143 0.000000000
## 191 V 1 0.150069231 236 237 24 0.000000000
## 192 V 3 0.276076882 194 195 134 0.000000000
## 193 <NA> NA NA NA 9 2.842131069
## 194 V 9 0.924490900 196 197 48 0.000000000
## 195 V 1 -0.126527401 210 211 86 0.000000000
## 196 V 1 -0.562247053 198 199 44 0.000000000
## 197 <NA> NA NA NA 4 2.557928653
## 198 V 2 0.921662358 200 201 15 0.000000000
## 199 V 4 0.063461054 204 205 29 0.000000000
## 200 V 2 -0.073666563 202 203 13 0.000000000
## 201 <NA> NA NA NA 2 -0.001233008
## 202 <NA> NA NA NA 7 0.381035910
## 203 <NA> NA NA NA 6 1.281298336
## 204 V 7 -0.543694073 206 207 17 0.000000000
## 205 V 3 0.006409995 208 209 12 0.000000000
## 206 <NA> NA NA NA 7 2.082875104
## 207 <NA> NA NA NA 10 1.414596639
## 208 <NA> NA NA NA 5 0.517814545
## 209 <NA> NA NA NA 7 1.425930355
## 210 V 4 0.835895726 212 213 37 0.000000000
## 211 V 3 0.709453728 224 225 49 0.000000000
## 212 V 4 -0.269537878 214 215 32 0.000000000
## 213 <NA> NA NA NA 5 1.008647127
## 214 V 9 0.677534260 216 217 15 0.000000000
## 215 V 4 0.624935172 220 221 17 0.000000000
## 216 V 9 0.166190376 218 219 11 0.000000000
## 217 <NA> NA NA NA 4 2.762488633
## 218 <NA> NA NA NA 7 1.473904804
## 219 <NA> NA NA NA 4 2.333795962
## 220 V 7 0.285653119 222 223 13 0.000000000
## 221 <NA> NA NA NA 4 0.678882941
## 222 <NA> NA NA NA 8 2.106691243
## 223 <NA> NA NA NA 5 0.496236762
## 224 <NA> NA NA NA 28 1.894484219
## 225 V 6 -1.105478996 226 227 21 0.000000000
## 226 <NA> NA NA NA 3 3.246087325
## 227 V 4 1.059238428 228 229 18 0.000000000
## 228 V 4 -0.480899694 230 231 17 0.000000000
## 229 <NA> NA NA NA 1 1.733109373
## 230 <NA> NA NA NA 4 1.723979096
## 231 V 4 -0.418572196 232 233 13 0.000000000
## 232 <NA> NA NA NA 1 1.265400523
## 233 V 6 -0.076132076 234 235 12 0.000000000
## 234 <NA> NA NA NA 3 3.949907056
## 235 <NA> NA NA NA 9 2.929014449
## 236 V 9 0.713825962 238 239 16 0.000000000
## 237 <NA> NA NA NA 8 2.837167998
## 238 V 9 -0.132071548 240 241 13 0.000000000
## 239 <NA> NA NA NA 3 3.887067036
## 240 <NA> NA NA NA 5 1.755728835
## 241 <NA> NA NA NA 8 2.824642864
## 242 <NA> NA NA NA 4 4.181286753
## 243 <NA> NA NA NA 7 2.775822127
## 244 V 9 1.238645228 246 247 29 0.000000000
## 245 V 9 0.404696084 254 255 23 0.000000000
## 246 V 9 0.063649950 248 249 25 0.000000000
## 247 <NA> NA NA NA 4 3.925580300
## 248 <NA> NA NA NA 8 2.162254340
## 249 V 7 -0.900734272 250 251 17 0.000000000
## 250 <NA> NA NA NA 3 2.495057397
## 251 V 4 -0.527972240 252 253 14 0.000000000
## 252 <NA> NA NA NA 4 3.024567839
## 253 <NA> NA NA NA 10 3.830827884
## 254 <NA> NA NA NA 10 3.632664827
## 255 V 5 -0.112974489 256 257 13 0.000000000
## 256 <NA> NA NA NA 6 5.679580559
## 257 <NA> NA NA NA 7 4.553183634
## 258 V 3 1.530286592 260 261 14 0.000000000
## 259 V 5 1.043822482 264 265 21 0.000000000
## 260 V 9 -0.110898622 262 263 13 0.000000000
## 261 <NA> NA NA NA 1 4.090908056
## 262 <NA> NA NA NA 3 2.442667057
## 263 <NA> NA NA NA 10 4.097267466
## 264 V 5 -0.772476544 266 267 19 0.000000000
## 265 <NA> NA NA NA 2 5.976713414
## 266 <NA> NA NA NA 7 4.880034990
## 267 V 4 0.402821807 268 269 12 0.000000000
## 268 <NA> NA NA NA 9 4.793675377
## 269 <NA> NA NA NA 3 6.759036121Check seed match
RLTrep <- RLT(X, y, model = "regression",
ntrees = 100, ncores = 1, nmin = 10,
split.gen = "random", nsplit = 1,
resample.prob = 0.85, resample.replace = FALSE,
reinforcement = TRUE, importance = "distribute",
param.control = list("embed.ntrees" = 50,
"embed.mtry" = 1/2,
"embed.nmin" = 5),
verbose = TRUE, seed = RLTfit$parameters$seed)
## Regression Random Forest ...
## ---------- Parameters Summary ----------
## (N, P) = (1000, 10)
## # of trees = 100
## (mtry, nmin) = (3, 10)
## split generate = Random, 1
## sampling = 0.85 w/o replace
## (Obs, Var) weights = (No, No)
## importance = distribute
## reinforcement = Yes
## ----------------------------------------
## embed.ntrees = 50
## embed.mtry = 50%
## embed.nmin = 5
## embed.split.gen = Random, 1
## embed.resample.replace = TRUE
## embed.resample.prob = 0.9
## embed.mute = 0
## embed.protect = 14
## embed.threshold = 0.25
## ----------------------------------------
all(RLTfit$VarImp == RLTrep$VarImp)
## [1] TRUELinear Combination Split
We can also use a linear combination of variables as the splitting rule, i.e.,
The search of top variables is the same embedded random forest, however,
is determined using other criteria such as the "naive"
appraoch proposed in the original paper (Zhu, et al. 2015), PCA
("pca"), linear regression ("lm") and sliced
inverse regression ("sir"). When a categorical variable is
encountered (random best at internal node), the algorithm switch to the
default single variable split.
# set.seed(1)
library(MASS)
ntrain = 300
ntest = 500
n = ntrain + ntest
p = 10
S = matrix(0.3, p, p)
diag(S) = 1
X1 = mvrnorm(n, mu = rep(0, p), Sigma = S)
X2 <- matrix(as.integer(runif(n * p) * 5), n, p)
# Combine continuous and categorical variables into a data frame (X)
X <- data.frame(X1, X2)
# Convert the second half of the columns in X to factors
X[, (p + 1):(2*p)] <- lapply(X[, (p+1):(2*p)], as.factor)
xlink <- function(x) 1 + x[, 1] + x[, 3] + x[, ncol(x)] %in% c(0,2,4)
# outcome
y = xlink(X) + rnorm(n)
w = runif(ntrain)
xtrain = X[1:ntrain, ]
ytrain = y[1:ntrain]
xtest = X[-(1:ntrain), ]
ytest = y[-(1:ntrain)]
start_time <- Sys.time()
RLTfit <- RLT(xtrain, ytrain, model = "regression", obs.w = w,
ntrees = 100, ncores = 1, nmin = 10, mtry = 10,
split.gen = "random", nsplit = 2,
resample.prob = 0.9, resample.replace = FALSE,
param.control = list("linear.comb" = 3,
"split.rule" = "naive",
"embed.ntrees" = 50,
"embed.mtry" = 0.5,
"embed.nmin" = 5,
"embed.split.gen" = "random",
"embed.nsplit" = 3,
"embed.resample.replace" = FALSE,
"embed.resample.prob" = 0.9,
"embed.mute" = 1/3,
"embed.protect" = 3,
"embed.threshold" = 0.25),
importance = "permute",
verbose = TRUE)
## Regression Forest with Linear Combination Splits ...
## ---------- Parameters Summary ----------
## (N, P) = (300, 20)
## # of trees = 100
## (mtry, nmin) = (10, 10)
## split generate = Random, 2
## sampling = 0.9 w/o replace
## (Obs, Var) weights = (Yes, No)
## linear combination = 3
## split rule = naive
## importance = permute
## reinforcement = No
## ----------------------------------------
difftime(Sys.time(), start_time, units = "secs")
## Time difference of 6.851847 secs
# oob prediction and error
plot(RLTfit$Prediction, ytrain)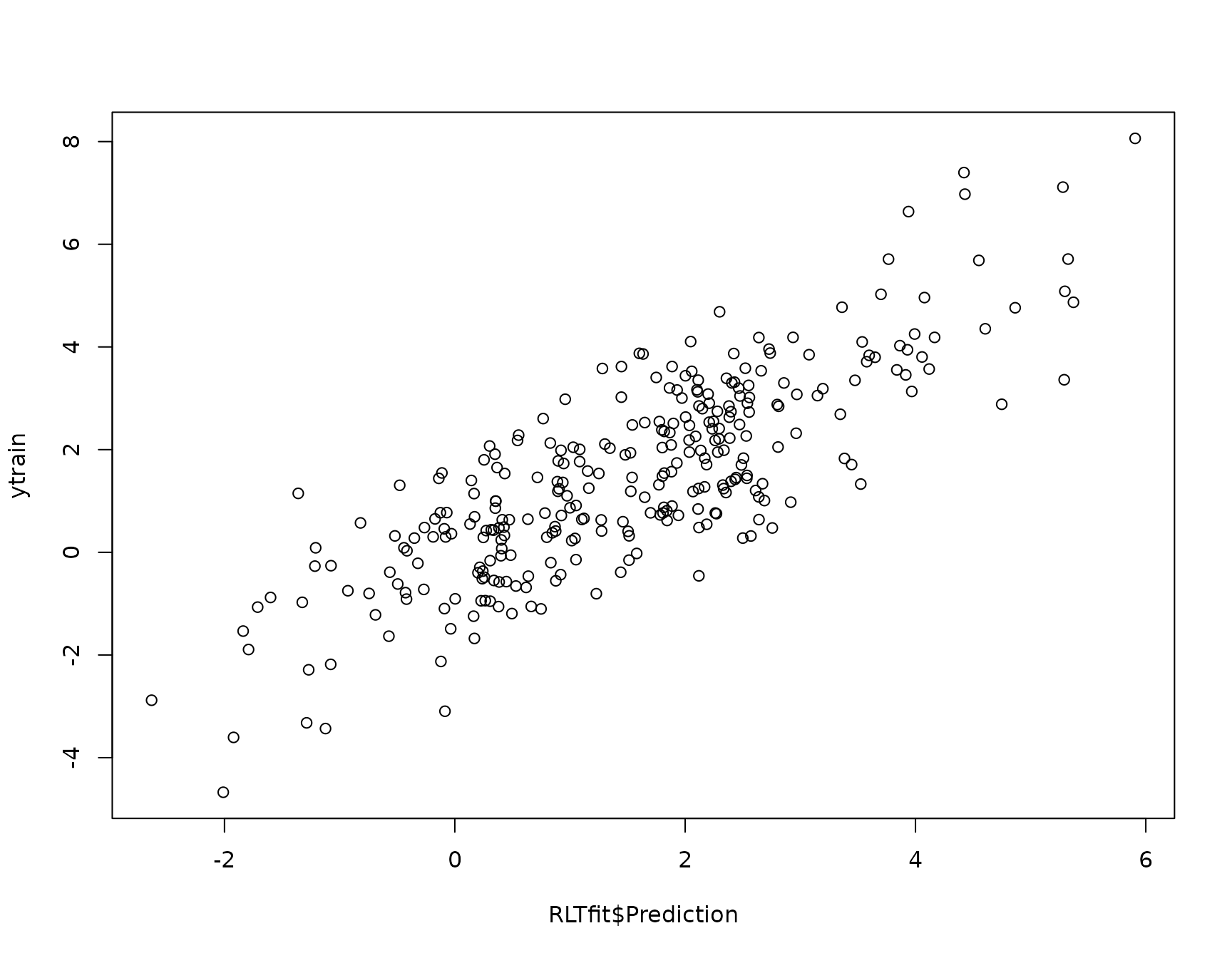
mean( (RLTfit$Prediction - ytrain)^2 , na.rm = TRUE)
## [1] 1.235547
# testing data error
mean((predict(RLTfit, xtest)$Prediction - ytest)^2)
## [1] 1.149594
start_time <- Sys.time()
RLTvi2 <- RLT(xtrain, ytrain, model = "regression", obs.w = w,
ntrees = 100, ncores = 1, nmin = 10, mtry = 10,
split.gen = "random", nsplit = 2,
resample.prob = 0.9, resample.replace = FALSE,
param.control = list("linear.comb" = 3,
"split.rule" = "sir",
"embed.ntrees" = 50,
"embed.mtry" = 0.5,
"embed.nmin" = 5,
"embed.split.gen" = "random",
"embed.nsplit" = 3,
"embed.resample.replace" = FALSE,
"embed.resample.prob" = 0.9,
"embed.mute" = 1/3,
"embed.protect" = 3,
"embed.threshold" = 0.25),
importance = "distribute",
verbose = TRUE)
## Regression Forest with Linear Combination Splits ...
## ---------- Parameters Summary ----------
## (N, P) = (300, 20)
## # of trees = 100
## (mtry, nmin) = (10, 10)
## split generate = Random, 2
## sampling = 0.9 w/o replace
## (Obs, Var) weights = (Yes, No)
## linear combination = 3
## split rule = sir
## importance = distribute
## reinforcement = No
## ----------------------------------------
difftime(Sys.time(), start_time, units = "secs")
## Time difference of 6.842688 secs
par(mfrow=c(1,2))
par(mar = c(1, 2, 2, 2))
# sparse variable importance
barplot(as.vector(RLTfit$VarImp), main = "RLT Permutation VI")
barplot(as.vector(RLTvi2$VarImp), main = "RLT Distributed VI")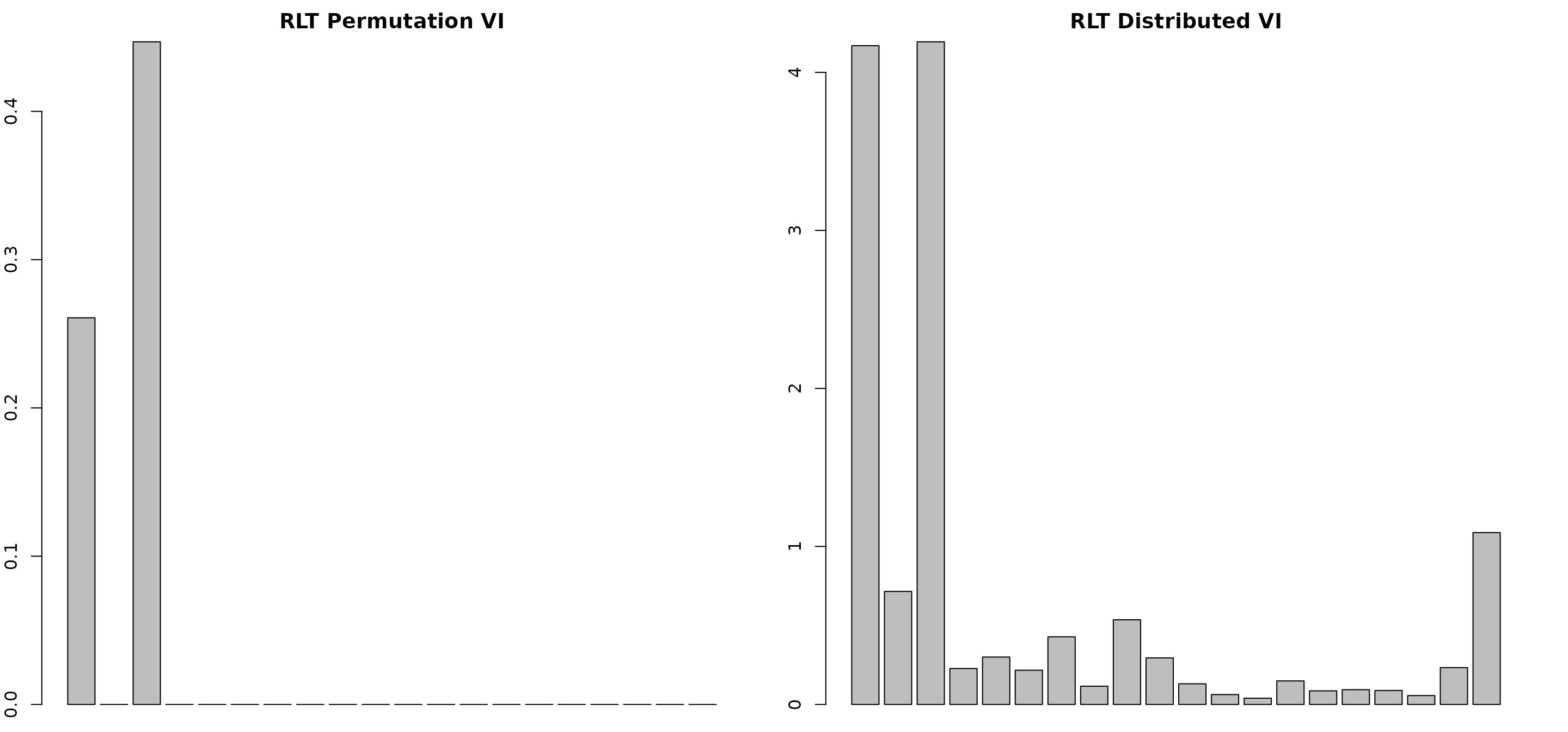
# check one tree
get.one.tree(RLTfit, 1)
## Tree #1 in the fitted linear combination regression forest:
## SplitVar.1 SplitVar.2 SplitVar.3 SplitLoad.1 SplitLoad.2 SplitLoad.3 SplitValue LeftNode RightNode NodeWeight NodeAve
## 1 X3 X1 1.3231691 1.23174687 0 -0.07706315 2 3 0.908612391 0.0000000
## 2 X1 X3 0.8274917 0.74400121 0 -0.18481930 4 5 0.422003759 0.0000000
## 3 X3 X1 0.9085061 0.77844733 0 0.61676199 26 27 0.486608632 0.0000000
## 4 X3 X1 0.7920686 0.74643704 0 -1.26713524 6 7 0.380656316 0.0000000
## 5 <NA> <NA> <NA> NA NA NA NA NA NA 0.041347443 1.5303985
## 6 X10.1 (F) 1.0000000 0.00000000 0 34.00000000 8 9 0.109248402 0.0000000
## 7 X10.1 (F) 1.0000000 0.00000000 0 40.00000000 16 17 0.271407914 0.0000000
## 8 X1 1.0000000 0.00000000 0 -1.57700855 10 11 0.062214882 0.0000000
## 9 X1 1.0000000 0.00000000 0 -1.35618526 14 15 0.047033519 0.0000000
## 10 <NA> <NA> <NA> NA NA NA NA NA NA 0.032011465 -2.6569265
## 11 X3 1.0000000 0.00000000 0 -2.34377950 12 13 0.030203418 0.0000000
## 12 <NA> <NA> <NA> NA NA NA NA NA NA 0.006914019 -2.7335368
## 13 <NA> <NA> <NA> NA NA NA NA NA NA 0.023289398 -0.8729562
## 14 <NA> <NA> <NA> NA NA NA NA NA NA 0.021295620 -0.4331007
## 15 <NA> <NA> <NA> NA NA NA NA NA NA 0.025737899 0.1901192
## 16 X10.1 (F) 1.0000000 0.00000000 0 2.00000000 18 19 0.191915479 0.0000000
## 17 X3 X10 0.4931212 0.43142204 0 -0.37759703 20 21 0.079492435 0.0000000
## 18 <NA> <NA> <NA> NA NA NA NA NA NA 0.141408082 0.1102366
## 19 <NA> <NA> <NA> NA NA NA NA NA NA 0.050507398 0.6981400
## 20 <NA> <NA> <NA> NA NA NA NA NA NA 0.022320250 1.4395327
## 21 X1 1.0000000 0.00000000 0 -0.54953057 22 23 0.057172185 0.0000000
## 22 X1 1.0000000 0.00000000 0 -1.63211666 24 25 0.047952749 0.0000000
## 23 <NA> <NA> <NA> NA NA NA NA NA NA 0.009219436 1.5860325
## 24 <NA> <NA> <NA> NA NA NA NA NA NA 0.011230709 1.7119574
## 25 <NA> <NA> <NA> NA NA NA NA NA NA 0.036722040 0.7172546
## 26 X7 1.0000000 0.00000000 0 -1.67131191 28 29 0.213692879 0.0000000
## 27 X1 X3 0.9747714 0.84941119 0 2.66452790 50 51 0.272915754 0.0000000
## 28 <NA> <NA> <NA> NA NA NA NA NA NA 0.014994611 0.9554701
## 29 X7 X2 -0.4209997 0.22710658 0 0.31062849 30 31 0.198698267 0.0000000
## 30 X7 1.0000000 0.00000000 0 1.87526053 32 33 0.153665240 0.0000000
## 31 <NA> <NA> <NA> NA NA NA NA NA NA 0.045033028 2.4412080
## 32 X7 1.0000000 0.00000000 0 0.79648732 34 35 0.147998682 0.0000000
## 33 <NA> <NA> <NA> NA NA NA NA NA NA 0.005666558 2.9048770
## 34 X5.1 (F) 1.0000000 0.00000000 0 60.00000000 36 37 0.101844543 0.0000000
## 35 X2 1.0000000 0.00000000 0 0.14897519 48 49 0.046154139 0.0000000
## 36 <NA> <NA> <NA> NA NA NA NA NA NA 0.015924004 1.4467864
## 37 X3 X1 0.4007989 -0.34891053 0 0.51704594 38 39 0.085920539 0.0000000
## 38 X7 X1 -0.2657772 0.25425640 0 0.14424181 40 41 0.079711804 0.0000000
## 39 <NA> <NA> <NA> NA NA NA NA NA NA 0.006208735 3.4318513
## 40 X3 X7 0.1431964 -0.13490213 0 0.04575013 42 43 0.054982336 0.0000000
## 41 <NA> <NA> <NA> NA NA NA NA NA NA 0.024729468 2.4318951
## 42 X1 1.0000000 0.00000000 0 0.60092053 44 45 0.044591402 0.0000000
## 43 <NA> <NA> <NA> NA NA NA NA NA NA 0.010390934 2.6567664
## 44 X7 X3 -0.1037545 -0.06234505 0 -0.05734202 46 47 0.032246716 0.0000000
## 45 <NA> <NA> <NA> NA NA NA NA NA NA 0.012344686 2.7439300
## 46 <NA> <NA> <NA> NA NA NA NA NA NA 0.004994244 1.7678419
## 47 <NA> <NA> <NA> NA NA NA NA NA NA 0.027252472 1.5191137
## 48 <NA> <NA> <NA> NA NA NA NA NA NA 0.023854892 0.7492995
## 49 <NA> <NA> <NA> NA NA NA NA NA NA 0.022299248 1.4490659
## 50 X3 X1 0.4206006 0.21512389 0 0.31635158 52 53 0.240125913 0.0000000
## 51 X1 X3 1.1773737 -1.09770251 0 -1.18651743 66 67 0.032789840 0.0000000
## 52 <NA> <NA> <NA> NA NA NA NA NA NA 0.038752381 2.1558582
## 53 X3 X1 0.7759470 0.50676296 0 1.32511136 54 55 0.201373532 0.0000000
## 54 X3 1.0000000 0.00000000 0 0.57031210 56 57 0.150660578 0.0000000
## 55 X3 1.0000000 0.00000000 0 2.45611914 62 63 0.050712954 0.0000000
## 56 X1 1.0000000 0.00000000 0 0.67884452 58 59 0.042563050 0.0000000
## 57 <NA> <NA> <NA> NA NA NA NA NA NA 0.108097528 2.7121510
## 58 <NA> <NA> <NA> NA NA NA NA NA NA 0.004856537 1.3274791
## 59 X1 X3 0.4855952 0.40446088 0 0.75671826 60 61 0.037706514 0.0000000
## 60 <NA> <NA> <NA> NA NA NA NA NA NA 0.023900269 2.3772008
## 61 <NA> <NA> <NA> NA NA NA NA NA NA 0.013806244 3.3803396
## 62 X3 X1 0.4581321 0.38550016 0 1.05865315 64 65 0.047123176 0.0000000
## 63 <NA> <NA> <NA> NA NA NA NA NA NA 0.003589778 6.6364296
## 64 <NA> <NA> <NA> NA NA NA NA NA NA 0.028595474 3.9662215
## 65 <NA> <NA> <NA> NA NA NA NA NA NA 0.018527702 4.3113683
## 66 <NA> <NA> <NA> NA NA NA NA NA NA 0.013614761 4.1598683
## 67 <NA> <NA> <NA> NA NA NA NA NA NA 0.019175079 7.1428770Linear combination kernel
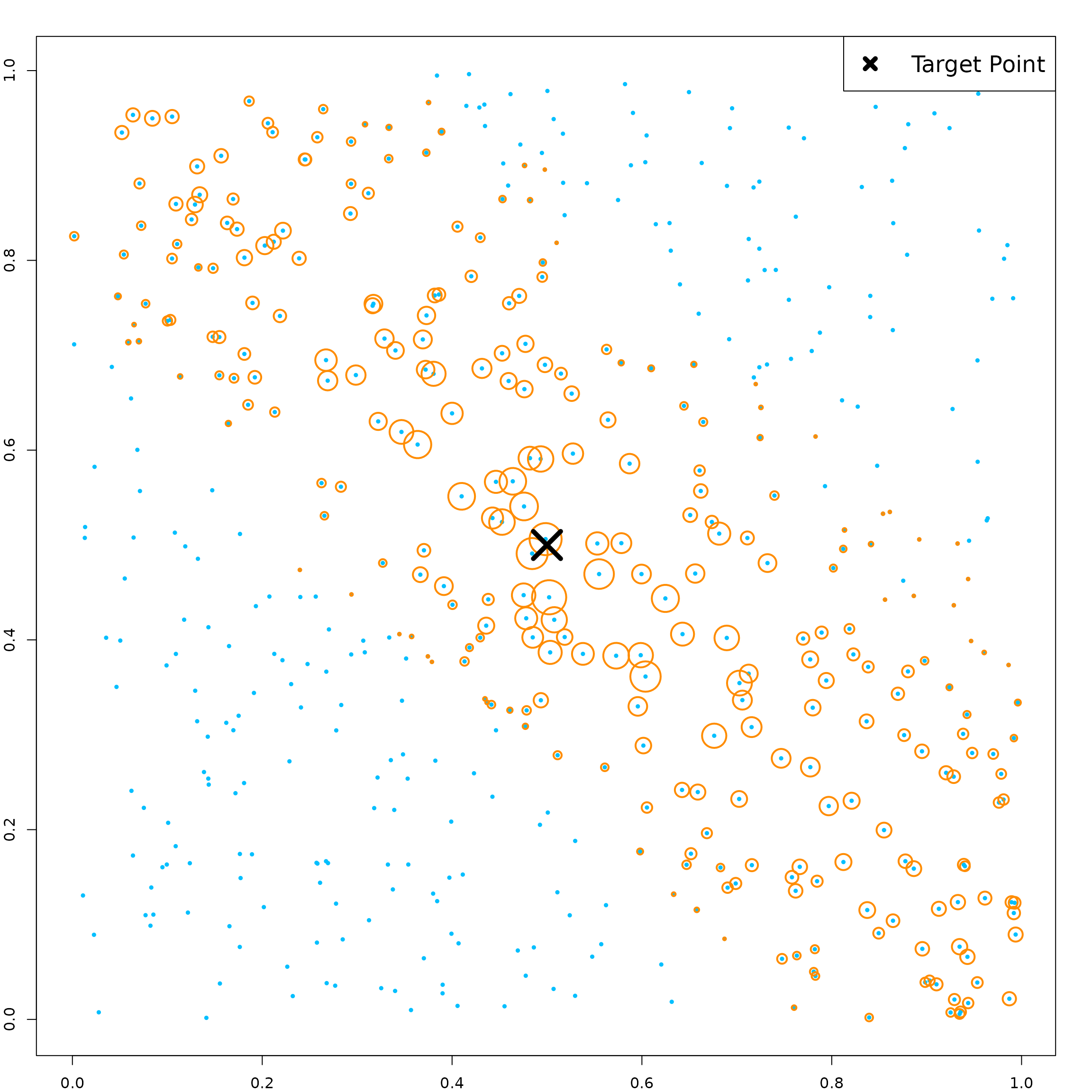
The linear combination split leads to non-rectangular kernels.
# generate data
set.seed(1)
n = 500; p = 5
X = matrix(runif(n*p), n, p)
y = X[, 1] + X[, 3] + 0.3*rnorm(n)
# fit model
RLTfit <- RLT(X, y, model = "regression",
ntrees = 300, ncores = 10, nmin = 15, mtry = 5,
split.gen = "random", nsplit = 3,
resample.prob = 0.9, resample.replace = FALSE,
param.control = list("embed.ntrees" = 50,
"linear.comb" = 3,
"embed.nmin" = 10,
"split.rule" = "naive",
"alpha" = 0.25),
verbose = TRUE)
## Regression Forest with Linear Combination Splits ...
## ---------- Parameters Summary ----------
## (N, P) = (500, 5)
## # of trees = 300
## (mtry, nmin) = (5, 15)
## split generate = Random, 3
## sampling = 0.9 w/o replace
## (Obs, Var) weights = (No, No)
## alpha = 0.25
## linear combination = 3
## split rule = naive
## importance = none
## reinforcement = No
## ----------------------------------------
## Do not have 10 cores, use maximum 4 cores.
# target point
newX = matrix(c(0.5, 0.5, 0.5, 0.5, 0.5),
1, 5)
# get kernel weights defined by the kernel function
KernelW = forest.kernel(RLTfit, X1 = newX, X2 = X)$Kernel
par(mar = c(2, 2, 2, 2))
plot(X[, 1], X[, 3], col = "deepskyblue", pch = 19, cex = 0.5)
points(X[, 1], X[, 3], col = "darkorange",
cex = 10*sqrt(KernelW/sqrt(sum(KernelW^2))), lwd = 2)
points(newX[1], newX[3], col = "black", pch = 4, cex = 4, lwd = 5)
legend("topright", "Target Point", pch = 4, col = "black",
lwd = 5, lty = NA, cex = 1.5)